Buscando los secretos de la Naturaleza

Hay que reconocer que algunas imágenes captadas por los telescopios son asombrosas

Las fuerzas fundamentales

Las constantes fundamentales

Unas pueden ser más constantes naturales que otras, pero lo cierto es que, de momento, han servido como herramientas eficaces.

La Constante de la Estructura Fina, un número fundamental que afecta al color de la luz emitido por los átomos y todas las interacciones químicas, no ha cambiado en más de siete mil millones de años, según observaciones hechas por un equipo de astrónomos que estudian la evolución de las galaxias y del universo.

La última lección importante que aprendemos de la manera en que números puros como α (alfa) definen el mundo, es el verdadero significado de que los mundos sean diferentes. El número puro que llamamos constante de estructura fina, e indicamos con α, es como hemos dicho antes, una combinación de e, c y h (el electrón, la velocidad de la luz y la constante de Planck). Inicialmente, podríamos estar tentados a pensar que un mundo en el que la velocidad de la luz fuera más lenta sería un mundo diferente. Pero sería un error. Si e, h y c cambian de modo que los valores que tienen en unidades métricas (o cualesquiera otras) fueran diferentes cuando las buscamos en nuestras tablas de constantes físicas, pero el valor de α permaneciera igual; este nuevo mundo sería observacionalmente indistinguible de nuestro mundo. Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza.

“La covariancia de Lorentz (y análogamente la contravariancia de Lorentz) o principio especial de la relatividad se refiere a la propiedad de ciertas ecuaciones físicas de no cambiar de forma bajo cambios de coordenadas de un tipo particular, concretamente es requisito de la teoría especial de la relatividad que las leyes de la Física tienen que tomar la misma forma en todos los marcos de referencia inerciales.”

Fue Einstein el que anunció lo que se llamó principio de covariancia: que las leyes de la naturaleza deberían expresarse en una forma que pareciera la misma para todos los observadores, independientemente de dónde estuvieran situados y de cómo se estuvieran moviendo. Cuando trató de desarrollar este principio, Einstein tuvo dificultades; no encontraba la manera de expresarlo con la formulación matemática adecuada. Pidió ayuda a su amigo Marcel Grossmann, matemático, quien sabiendo de las necesidades exactas de Einstein, le envió la copia de una conferencia que dio un tal Riemann, unos sesenta años antes.

Einstein fue muy afortunado, ya que durante la última parte del siglo XIX en Alemania e Italia, matemáticos puros habían estado inmersos en el estudio profundo y detallado de todas las geometrías posibles sobre superficies curvas. Habían desarrollado un lenguaje matemático que automáticamente tenía la propiedad de que toda ecuación poseía una forma que se conservaba cuando las coordenadas que la describían se cambiaban de cualquier manera. Este lenguaje se denominaba cálculo tensorial. Tales cambios de coordenadas equivalen a preguntar qué tipo de ecuación vería alguien que se moviera de una manera diferente.

Einstein se quedó literalmente paralizado al leer la Conferencia de Riemann. Allí, delante de sus propios ojos tenía lo que Riemann denominaba Tensor métrico. Einstein se dio cuenta de que era exactamente lo que necesitaba para expresar de manera precisa y exacta sus ideas. Así  llegó a ser  posible la teoría de la relatividad general.

Einstein pudo expresar su principio de covariancia expresando sus leyes de la naturaleza como ecuaciones tensoriales, que poseían automáticamente la misma forma para todos los observadores.

Con este “esqueleto” procedemos a escribir adentro del espacio vacío uno a uno los componentes del tensor de curvatura de Einstein. Podemos escribirlos como los componentes de un tensor covariante de orden dos, los componentes de un tensor mixto, o los componentes de un tensor contravariante de orden dos, todo es cuestión de gustos que al fin y al cabo podemos “subir” y “bajar” los índices a nuestro antojo con la ayuda del tensor métrico g. Lo haremos aquí representándolos como los componentes contravariantes de un tensor de orden dos:

Esto automáticamente nos fija la manera en la cual tenemos que escribir los componentes del tensor energía-tensión T, también como componentes de un tensor contravariante de orden dos, dada la igualdad tensorial:

Este paso de Einstein completó un movimiento espectacular en la concepción física de la naturaleza que ha sido completado en el siglo XX. Está marcado por una evolución que se aleja continuamente de cualquier visión privilegiada del mundo, sea una visión humana, basada en la Tierra, o una visión basada en patrones humanos, la naturaleza tiene sus propios patrones.

Las estrellas y los mundos se forman de la misma manera en todas las regiones del Universo

Está claro que pensar siquiera enue en nuestro universo, dependiendo de la región en la que nos encontremos, habrá distintas leyes físicas, sería pensar en un universo chapuza. Lo sensato es pensar como Einstein y creer que en cualquier parte del universo rigen las mismas leyes físicas, hasta que no se encuentre pruebas reales a favor de lo contrario,  los científicos suponen con prudencia que, sea cual fueren las causas responsables de las pautas que llamamos “Leyes de la Naturaleza”, es mucho más inteligente adoptar la creencia de la igualdad física en cualquier parte de nuestro universo por muy remota que se encuentre; los elementos primordiales que lo formaron fueron siempre los mismos que interaccionan con las cuatro fuerzas fundamentales naturales.

                          También ahí están presentes las fuerzas naturales

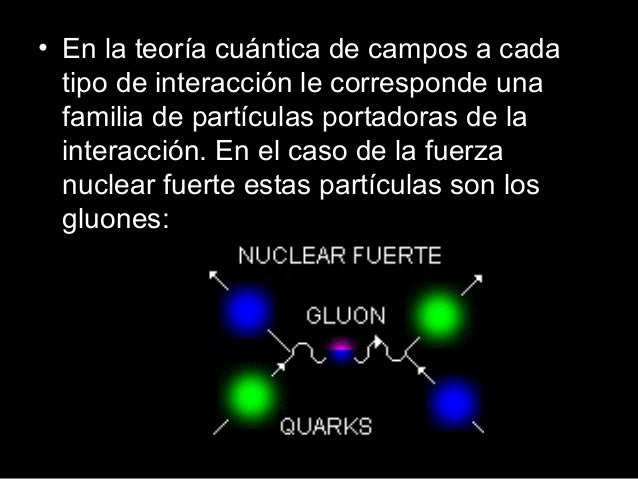
Ahora sabemos que las fuerzas de la naturaleza, la fuerza nuclear fuerte, la fuerza nuclear débil, el electromagnetismo y la gravedad, no son tan diferentes como parece a primera vista. Parecen tener intensidades muy diferentes y actuar sobre partículas elementales diferentes. Pero eso es ilusorio, es la sensación creada por nuestra necesidad de habitar en un lugar del universo donde la temperatura es más bien baja y, es así, como se manifiestan las fuerzas de la naturaleza que, en dicha temperatura permite la existencia de átomos y moléculas.

se necesitaría una fila de diez millones para llenar el espacio de un milímetro, y, también puede sorprender que las moléculas sean saltarinas

Conforme la temperatura aumenta y las partículas elementales de materia colisionan entre sí a energías cada vez más altas, las fuerzas separadas que gobiernan nuestro mundo de baja temperatura, se hacen más parecidas. La fuerza fuerte se debilita, la fuerza débil aumenta y fortalece. Aparecen nuevas partículas a medida que se alcanzan temperaturas más elevadas y consiguen producir interacciones entre las familias separadas de partículas que a temperaturas bajas, parecen estar aisladas entre sí.

Poco a poco, a medida que nos acercamos a esas inimaginables condiciones de temperatura “última” que Max Planck encontró definida por las cuatro constantes de la naturaleza, G, K, c, h, esperamos que las diferencias entre las fuerzas naturales se vayan borrando completamente para finalmente quedar unificadas en una única fuerza como, por otra parte, se cree que fue al principio de todo, cuando en el Big Bang, el proceso ocurrió al contrario. Había una increíble temperatura, un plasma primordial lo invadía todo y se expansionaba, naciendo el tiempo y el espacio cuando reinaba la simetría total y una sola fuerza lo regía todo.

El universo continuó su expansión y comenzó a enfriarse, la simetría se rompió y lo que era una sola fuerza se dividió en las cuatro que ahora conocemos. Previamente, a partir del plasma, al bajar la temperatura, surgieron los quarks que se juntaron para formar protones y neutrones que, a su vez, se juntaron para formar núcleos que, al ser rodeados por los electrones atraídos por la carga positiva de los núcleos, formaron los átomos, que se unieron para formar moléculas, que se juntaron para formar la materia, que más tarde, dio lugar al nacimiento de las primeras estrellas y galaxias con sus variedades de objetos estelares, planetas, satélites, cometas, meteoritos, etc.

¡El Universo! ¿Cuándo lo podremos comprender?

emilio silvera

Compartelo:

[?]