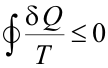Variación de entropía del universoDesde el punto de vista de la Termodinámica, el universo es el conjunto constituido por un sistema y sus alrededores. Es, por tanto, un sistema aislado (no hay nada fuera de él). De la misma manera en que se puede calcular la variación de entropía de un sistema termodinámico entre dos estados, puede calcularse la variación de entropía de sus alrededores (todo lo que ha interaccionado con nuestro sistema). La suma de ambas magnitudes se denomina variación de entropía del universo. Como el universo es un sistema aislado, utilizando el teorema de Clausius se tiene que, para el universo:
|
Donde el signo igual es aplicable para una transformación reversible y el signo menor que cuando dicha transformación es irreversible. A continuación se analiza cada caso por separado. En todo proceso irreversible, la entropía del universo aumenta. “Los sistemas aislados al evolucionar, tienden a desordenarse, nunca a ordenarse”. La entropía entropía mide el grado de desorden o de orden del sistema y depende únicamente de los estados inicial y final de dicho sistema. En todo proceso irreversible, la entropía del universo aumenta. “Los sistemas aislados al evolucionar, tienden a desordenarse, nunca a ordenarse”. La entropía entropía mide el grado de desorden o de orden del sistema y depende únicamente de los estados inicial y final de dicho sistema.
En el siguiente diagrama p – V se ha representado un ciclo irreversible
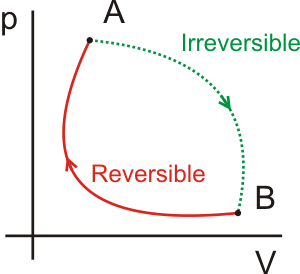
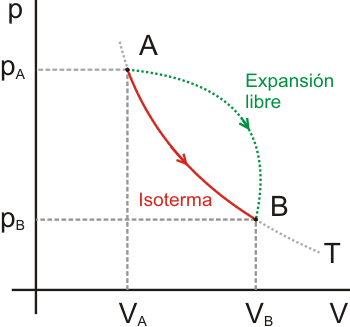
Está constituido por dos transformaciones: la AB (representada en verde en la figura), que es irreversible, y la BA (en rojo) que es reversible. Como el ciclo en su conjunto es irreversible, debemos aplicar el teorema de Clausius con el signo menor:
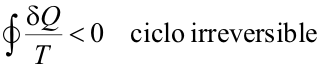 |
La integral de línea que aparece en la ecuación anterior puede ser descompuesta en la suma de las integrales evaluadas en cada etapa del ciclo, quedando:


Así

En todo proceso irreversible, la entropía del universo aumenta. “Los sistemas aislados al evolucionar, tienden a desordenarse, nunca a ordenarse”. La entropía entropía mide el grado de desorden o de orden del sistema y depende únicamente de los estados inicial y final de dicho sistema.
Ya que la integral evaluada a lo largo del tramo reversible es precisamente la variación de entropía entre los estados B y A. Por tanto,
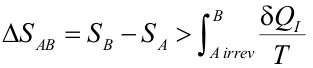 |
Expresión conocida como desigualdad de Clausius.
El significado físico de esta ecuación es que la variación de entropía entre dos estados cualesquiera será siempre mayor que la integral del calor intercambiado irreversiblemente entre los dos estados partido por la temperatura.
Como aplicación de esta expresión, la variación de entropía en la expansión libre de Joule ha de ser mayor que cero (como efectivamente lo es) ya que el calor intercambiado en esta transformación irreversible es cero.
Como el universo es un sistema aislado, cuando en el universo se produce una transformación cualquiera AB irreversible el calor intercambiado es cero, por lo que:
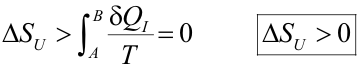 |
Es decir, la entropía del universo siempre crece para cualquier transformación irreversible que se produzca.

Cuando en el universo tiene lugar una transformación reversible, debemos tomar el signo igual:
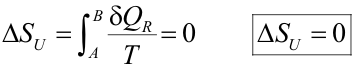 |
Agrupando ambos resultados:
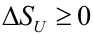 |
Esta afirmación constituye un nuevo enunciado del Segundo Principio:
|
La entropía es una función de estado que, evaluada para todo el universo, aumenta en una transformación irreversible y permanece constante en una transformación reversible.
La entropía nos lleva al desorden En física se habla de entropía (usualmente simbolizada con la letra S) para referirnos al grado de equilibrio de un sistema termodinámico, o más bien, a su nivel de tendencia al desorden (variación de entropía). Cuando se produce una variación de entropía positiva, los componentes de un sistema pasan a un estado de mayor desorden que cuando se produce una entropía negativa. La entropía es un concepto clave para la Segunda Ley de la termodinámica, que establece que “la cantidad de entropía en el universo tiende a incrementarse en el tiempo”. O lo que es igual: dado un período de tiempo suficiente, los sistemas tenderán al desorden. Ese potencial de desorden será mayor en la medida en que más próximo al equilibrio se halle el sistema. A mayor equilibrio, mayor entropía. También puede decirse que la entropía es el cálculo de la energía interna de un sistema que no es útil para realizar un trabajo, pero que existe y se acumula en un sistema determinado. Es decir, la energía excedente, desechable.
Cuando un sistema pasa de un estado inicial a uno secundario, en un proceso isotérmico (de igual temperatura), la variación de entropía (S2 – S1 ) será igual a la cantidad de calor que intercambie el sistema con el medio ambiente ,(Q1→ Q2 ), dividido por su temperatura. Esto se expresa según la siguiente ecuación: S2 – S1 = (Q1→ Q2)/ T Esto demuestra que solo se pueden calcular las variaciones de entropía en un sistema y no valores absolutos. El único punto en donde la entropía es nula es en el cero absoluto (0 K o -273,16 °C). A todo esto:
|
La Fuente está en un trabajo sobre Termodinámica